Bezier splines are great for artists, but they have some interesting technical challenges. One is that they are parametric: rather than y = f(x) as we would like, they are { x = f(t), y = f(t) }. Among other things, this means they can easily go backwards in time:

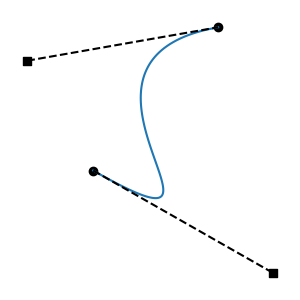
Such curves are non-functions: given a time, there is more than one possible value. This is intolerable for a system that governs values over time. We call these regressive segments. They are mathematically non-monotonic in the time dimension.

Artists probably don't create regressive curves on purpose. But they can certainly create them by accident. Splines can also be transformed, or generated programmatically, and this can lead to unusual cases.

Several different strategies have emerged for preventing regression. Ts splines take the following approach:

Encourage clients to prevent regression at authoring time. This ensures that all other clients will see exactly the same splines.
Provide several different implementations for anti-regression at authoring time. Allow spline-authoring clients to choose anti-regression modes that are consistent with their own behavior.
Support anti-regression during interactive edits, during spline modification via the API, and via bulk functions that operate on entire layers or stages.
Perform just-in-time anti-regression at evaluation time when regressive splines do manage to find their way into content. Use a single fixed anti-regression mode for this runtime behavior.

When Regression Arises

When addressing regression, we are only concerned with x(t), not with y(t). This means we only care about the placement of the control points in the time dimension. Anything can change in the value dimension, and what happens in the time dimension won't change at all. This is because x(t) and y(t) are separate functions. Changing values will squash, stretch, and skew the curve in the value dimension, but that doesn't matter for the question of regression.

We can also work in a normalized interval, scaled and translated so that the start knot is at time 0 and the end knot at time 1. This also has no effect on regression. The end result is that we care only about two numbers: the time coordinates of the knot tangent endpoints, expressed relative to the normalized interval.

If knot tangents don't leave the segment interval, we are guaranteed there is no regression. This is also intuitive for artists. It's a conservative rule you can learn: don't let a tangent cross the opposite knot, and you'll never get regression.

If both tangents alight exactly at the opposite knot, we get a single vertical, the limit of non-regression. (Throughout this document, we use "vertical" in the sense of "when graphed with time on the horizontal axis".)

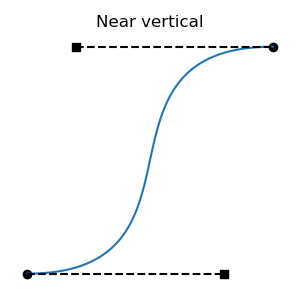
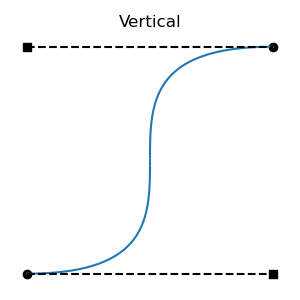
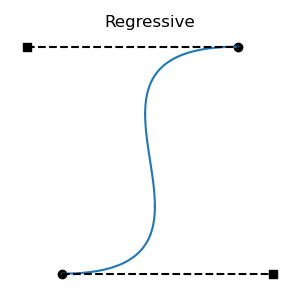
All regressive cases have at least one tangent outside the interval. Is the converse also true: that all cases with a tangent outside the interval are regressive? No: there are non-regressive curve shapes that can only be achieved by placing one of the tangent endpoints outside the interval. This can be non-regressive if the out-of-bounds tangent isn't too long, and the segment's other tangent is short enough. These cases are fairly atypical, involving regions of rapid change, but they are valid functions:

There's a graph that describes when regression arises:

In the green square, we have contained tangents, and there is no regression.
In the orange ellipse sections, we have bold tangents, and there is no regression.
On the red ellipse edge, we have a single vertical, and there is no regression.
Everywhere else, we have regression.
The ellipse also continues inside the green square, but it isn't meaningful there.

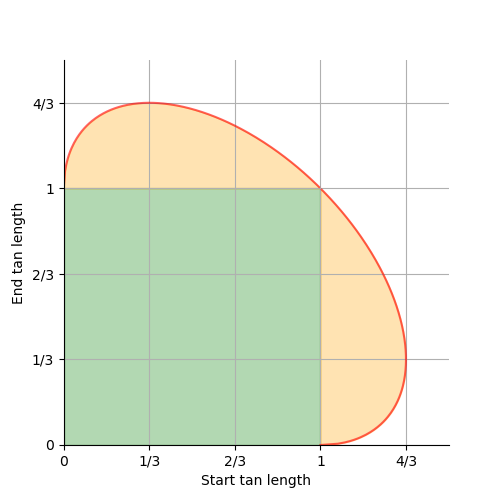
We've seen the (1, 1) point on the ellipse above; it's the symmetrical case with the vertical in the center of the interval. That one is also a corner of the green box, one of the limits of contained tangents.

Here are two additional important cases, the (1/3, 4/3) and (4/3, 1/3) ellipse limits. These are the longest possible non-regressive tangents. They put the vertical at times 1/9 and 8/9 respectively.

As we move between the above two limits, in the center of the ellipse edge, we make one tangent longer and the other shorter. As we move between the (4/3, 1/3) limits and the (1, 0) limits, at the fringes of the ellipse edge, we make both tangents longer or shorter.

At (0, 1) and (1, 0), we get a vertical at either endpoint. These are also at corners of the green square, and limits of contained tangents.

Interactive Anti-Regression Demo

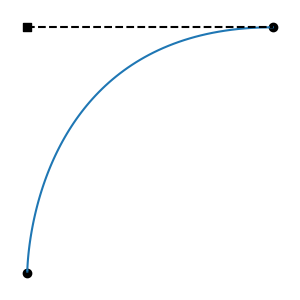
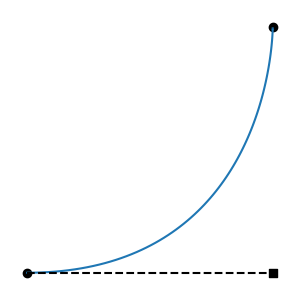
While reviewing the anti-regression strategies listed next, developers are encouraged to run regressDemo.py in the ts/script directory. This must be run by a Python interpreter than can import Ts, and either PySide6 or PySide2. Select a mode, then drag a tangent long, and watch the limiting behavior and the graph at the bottom.

Anti-Regression Strategies

First, most spline animation systems observe one important restriction, which Ts enforces as well: tangents may never face backwards, out of their segment's interval. Such a tangent will be ignored at runtime, as though it were zero-length. This prevents some of the worst cases. But, even when forced to face into their segments, tangents can cause regression by being too long.

Here are the anti-regression strategies that Ts supports:

Single-Tangent Strategies: shorten each tangent in isolation.

Contain: Forbid tangents from crossing neighboring knots in the time dimension. This is overly conservative: it forbids bold tangents, which is both a slight creative limitation and a possible point of incompatibility. But the system is simple and intuitive, and it is used in some popular packages.

Dual-Tangent Strategies: for each spline segment, consider both tangents, and shorten one or both.

Keep Start: When tangents are long enough to cause regression, keep the start tangent the same, and shorten the end tangent until the non-regressive limit is reached, with a single vertical. This is what Maya does. It's asymmetrical, always favoring the start tangent, a bias that often pushes the adjusted curve far to the right of the original regressive Bezier. On the ellipse graph above, Maya finds the vertical line through the original point in tangent-length space, and takes the nearest intersection with the ellipse. If the start tangent length is greater than 4/3, Maya alters both tangent lengths, always to (4/3, 1/3). The latter case is illustrated by this particular segment:

Keep Ratio: When tangents are long enough to cause regression, shorten both of them, until the non-regressive limit is reached, with a single vertical. In so doing, preserve the ratio of the original tangent lengths. On the ellipse graph above, this strategy finds the line from the origin to the original point, and takes the intersection of that line with the outer edge of the ellipse.

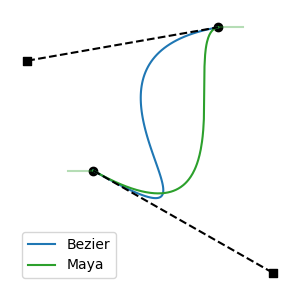
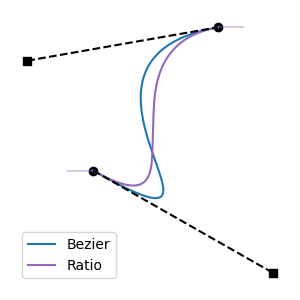
Interactive Strategies: as knots are interactively edited, clamp tangent lengths. Operate on both segments adjacent to the knot being edited. Handle edits to knot time, and edits to tangent length. These strategies only work during interactive edits, because they require differentiating between the knot being edited (the "active" knot) and the other knot in the segment (the "opposite" knot).

Limit Active: Clamp the active tangent to the non-regressive limit, given the existing length of the opposite tangent.
Limit Opposite: As the non-regressive limit is exceeded, shorten the opposite tangent to barely maintain non-regression. When the opposite tangent cannot be made any shorter without regression, clamp the active tangent there.

Disabling: If desired, regressive splines may be deliberately authored by selecting the None strategy. This will result in Keep Ratio behavior at evaluation time.

Center and Fringe Behavior

When the Limit Opposite mode is used, there are two slightly different behaviors:

When the opposite tangent starts out long (more than 1/3 of the interval), and the active tangent is dragged long enough to cause regression: the opposite tangent will be shortened until the (4/3, 1/3) maximum is reached, then stop there. In regressDemo, the way this behavior looks in the tangent-length graph is that the point collides with the center of the edge of the ellipse, then slides down it.
When the opposite tangent starts out short (less than 1/3 of the interval), and the active tangent is dragged long enough to cause regression: the opposite tangent will not be adjusted. This avoids the counter-intuitive result of lengthening the opposite tangent. In regressDemo, the way this behavior looks in the tangent-length graph is that the point collides with the fringe of the edge of the ellipse, and stops there.

With Keep Start, manipulating the length of the start tangent (but not the end tangent; recall that Keep Start is asymmetrical) behaves similarly to Limit Opposite, as described above. However, in the fringe case, the opposite tangent will in fact be lengthened until the (4/3, 1/3) maximum is reached. This is for compatibility with Maya.

API

Anti-Regression Contexts

Anti-regression is performed in the following ways:

Interactive Limiting: Clients that support interactive dragging of knots and tangent handles may use TsRegressionPreventer to filter edits.
Edit Limiting: Any time a TsSpline's knots are changed, regression is avoided by shortening tangents, if needed. The only two methods that can introduce regression are SetKnot and SwapKnots.
Querying: To determine if splines contain regressive segments, clients may call TsSpline::HasRegressiveTangents, UsdUtilsDoesLayerHaveRegressiveSplines, or UsdUtilsDoesStageHaveRegressiveSplines.
Explicit Limiting: If there is a possibility that a spline has been authored without anti-regression, clients may call TsSpline::AdjustRegressiveTangents.
Bulk Limiting: When splines are imported in USD content, and there is a possibility that those splines could have been generated without anti-regression, clients may call UsdUtilsAdjustRegressiveSplinesInLayer or UsdUtilsAdjustRegressiveSplinesOnStage.
Runtime Limiting: When splines are authored without anti-regression, and not subsequently de-regressed, and then evaluated, they will be de-regressed using the Keep Ratio strategy before evaluation. This evaluation-time behavior does not modify the spline in memory; it only modifies a temporary copy that is used for evaluation.

Current Authoring Mode

Ts always maintains a current authoring mode that affects all of the above operations, except for Runtime Limiting, which always uses Keep Ratio.

Default Authoring Mode

The (default) default anti-regression authoring mode is hard-coded to Keep Ratio. A different default may configured into the build:

With build_usd.py: --default-anti-regression=TsAntiRegression...
With cmake: -DPXR_TS_DEFAULT_ANTI_REGRESSION_AUTHORING_MODE=TsAntiRegression...

Authoring Mode Overrides

Clients may temporarily change the current authoring mode using TsAntiRegressionAuthoringSelector.

Contain Mode

The Contain mode, unlike all others, is conservative: it disallows some non-regressive splines (those with "bold" tangents that exceed the segment interval).

When the current authoring mode is Contain, all anti-regression operations will behave as though bold tangents were regressive. For example, TsSpline::HasRegressiveTangents will return true for bold tangents, and edit limiting will clamp tangents to the segment interval when knots are changed.

If clients use Contain mode by default, but wish to avoid this conservative behavior in some contexts, they may use a TsAntiRegressionAuthoringSelector to query and limit in a non-conservative mode, such as Keep Ratio.

Interactive Modes

TsRegressionPreventer supports all values of TsAntiRegressionMode. It also supports Limit Active and Limit Opposite, which cannot be used in any other context, because they require differentiating a single knot that is being edited.

It make sense to use TsRegressionPreventer in the same default mode as all other anti-regression contexts. It can also make sense to use Limit Active or Limit Opposite with TsRegressionPreventer, despite the default mode being different. Maintainers of client code are encouraged to try regressDemo to see what feels best.

Load-Time Policies

It is possible, using the bulk API in UsdUtils, to perform anti-regression at the time that spline content is loaded. Whether that is necessary depends on the client's situation.

If the content being loaded was generated by the same software that is now loading it, then the client can be sure that no regression has been introduced, and load-time anti-regression can be skipped.
If the content being loaded may have been generated by other software, the client has several options:
- Skip load-time anti-regression, because the ecosystem of software that may have generated the content faithfully observes anti-regression authoring.
- Skip load-time anti-regression, because it is preferable not to make automatic edits to imported content. If there are regressive splines, they will be de-regressed at evaluation time. If edits are made to regressive splines, they will undergo anti-regression at that time, which may cause additional changes on top of what the client is altering.
- Perform load-time anti-regression, because it is preferable to avoid unexpected changes at edit time.
If the content being loaded may have been generated by other software, and the client uses Contain mode, then it is possible that there are splines with bold tangents, which the client itself would never author. Clients may:
- Skip load-time anti-regression, because the client can tolerate bold tangents, and it is preferable not to change the shapes of imported splines.
- Perform load-time anti-regression, because the client prefers to ensure that all tangents are contained within the interval.

Note that load-time anti-regression is similar to load-time spline reduction, in which splines that use features that the client does not support can be converted to similar splines that emulate those features. If clients need both reduction and anti-regression, they will typically do both at the same time.